
 やすたん
tide736@gmail.com
やすたん
tide736@gmail.com

海上でのSOSに、電話による緊急番号は次のような場合に通報してください。
以上の場合において、「いつ」、「どこで」、「なにがあった」などを簡潔に落ち着いて通報してください。
航海の用に供する公式の潮汐の推算は、航海等における混乱を防ぐため、各国の水路機関が責任を持って行うことになっており、海上保安庁海洋情報部で毎年刊行している「潮汐表」が公式の潮汐推算値です。従って、本サイトが書誌742号「日本沿岸潮汐調和定数表」(平成4年2月発刊)から計算した結果は、「潮汐表」の代替物にはなりません。航海には必ず海上保安庁海洋情報部の「潮汐表」をご使用ください。

潮汐APIサービスは、日本沿岸736港の潮汐データを提供しています。
notification_important 本プログラムのご利用については一切のサポートをしておりません。
notification_important 一日のアクセス数を制限させていただく場合があります。
notification_important 予告なく変更・配信を終了する場合があります。あらかじめご了承下さい。
info 専用サーバー(ビジネスプラン)を設けてのAPIサービス提供も行っております。
JSONデータをリクエストする際のベースとなるURLは以下になります。
https://api.tide736.net/get_tide.php
info SSL接続とします。
下記のパラメータをセットし、POSTまたはGET送信でリクエストします。
| pc | 都道府県コード |
|---|---|
| hc | 港コード |
| yr | 調べたい年 |
| mn | 調べたい月 |
| dy | 調べたい日 |
| rg |
|
取得したJSONデータは以下の定義に基づいて構成されています。
| status | 応答ステータス | 0:異常終了/1:正常終了 | |||||
|---|---|---|---|---|---|---|---|
| message | 応答メッセージ | ||||||
| tide | port 港情報 |
prefecture_code | 都道府県コード | ||||
| harbor_code | 港コード | ||||||
| harbor_namej | 港名 | ||||||
| latitude | 緯度 | ||||||
| longitude | 経度 | ||||||
| level | 平均水面 | ||||||
| harbor_name | 港名(ローマ字) | ||||||
| tide_type | 潮汐タイプ | 1:長期観測/2:短期観測 | 長期観測とは1年単位での観測。短期は1ヶ月単位での観測 | ||||
| calc_time | 観測期間 | ||||||
| sa_ssa | 観測時期 | ||||||
| calc_way | 計算方法 | ||||||
| observe_public | 観測機関 | ||||||
| calc_public | 計算機関 | ||||||
| link リンク情報 |
prefecture_code | 都道府県コード | |||||
| harbor_code | 港コード | ||||||
| harbor_namej | 港名 | ||||||
| latitude | 緯度 | ||||||
| longitude | 経度 | ||||||
| tide_type | 潮汐タイプ | 1:長期観測/2:短期観測 | 長期観測とは1年単位での観測。短期は1ヶ月単位での観測 | ||||
| chart 潮汐情報 |
YYYY-MM-DD | sun 太陽情報 |
astro_twilight | 天文薄明 | 空の明るさが星明かりより明るい | ||
| regular_twilight | 常用薄明 | 灯火なしで屋外の活動ができる。市民薄明とも言います。 | |||||
| rise | 日の出時刻 | HH:MM | |||||
| midline | 正中時刻 | HH:MM | |||||
| set | 日の入時刻 | HH:MM | |||||
| moon 月情報 |
brightness | 輝面 | 月の明るさ | ||||
| age | 月齢 | ||||||
| title | 潮名 | 大潮/中潮/小潮/長潮/若潮/中潮/大潮/中潮/小潮/長潮/若潮/中潮/大潮 | この順序で切り替わります。 | ||||
| rise | 月の出時刻 | DD日 HH:MM | |||||
| midline | 正中時刻 | DD日 HH:MM | |||||
| set | 月の入時刻 | DD日 HH:MM | |||||
| name | 呼名 | 朔/上弦/望/下弦/朔 | |||||
| edd 干潮情報 |
time | 干潮時刻 | HH:MM | ||||
| unix | 干潮時刻 | UNIX時間 | UNIX時間に1000を乗算 | ||||
| cm | 干潮水位 | cm | |||||
| flood 満潮情報 |
time | 満潮時刻 | HH:MM | ||||
| unix | 満潮時刻 | UNIX時間 | UNIX時間に1000を乗算 | ||||
| cm | 満潮水位 | cm | |||||
| tide 潮汐情報 |
time | 時刻 | HH:MM | ||||
| unix | 時刻 | UNIX時間 | UNIX時間に1000を乗算 | ||||
| cm | 水位 | cm | |||||
info プロパティ名は順不同。
info 細かい部分は、下記「実際のJSONデータ」を参照ください。
潮汐画像API。ご自身のサイトにカンタンに潮汐画像を貼り付けることが出来ます。
insert_emoticon 設定内容は徐々に増やす予定です。

(潮汐計算略説は、書誌742号「日本沿岸潮汐調和定数表」の内容を転写しております。 出所を明記する事で許可頂けました。海上保安庁様に感謝です。)
潮汐とは、海面の規則的な周期的昇降を言う。
風浪や高潮などは、規則的かつ周期的ではないから、潮汐には含まれない。
自然現象で規則的かつ周期的なものといえば、月や太陽などの天体の運行であり、潮汐とは、以下に述べるように地球と月や太陽の公転および地球の自転によって生ずる海面の昇降を言う。
自転のことは後から考えることにして、地球と月の公転を考える。(図1)
地球とつきは、それぞれ両者の共通重心Gの周りを公転する。
この運動を支える向心力は、万有引力Fで、
(1)F=G・M・E/d2
と表される。
ここで、Gha万有引力定数、Mは天体の質量、Eは地球の質量、dは月の重心から地球の重心までの距離である。
地球の単位あたりの質量にすると、
(2)fd=G・M/d2
となる。
ここで、地球の表面上にある質点の動きを考えてみると、この質点の軌跡は、地球の重心と平行に同じ半径の円を描く。(図2)
この動きにつれて、この質点には、地球の重心に働いている向心力と同じ大きさで反対向きの遠心力が働く。
地球は、同じ形を保って公転運動を続けているから、この遠心力の大きさと向きは地球上どこでも同じである。
一方、この質点にはつきからの直接的な引力も働き、
図1
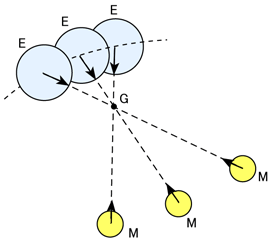
図2、地球の表面上にある質点の軌跡との遠心力
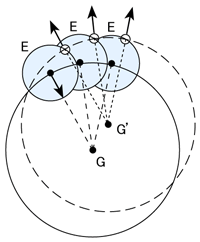
図3、月の引力と遠心力の差が潮汐力
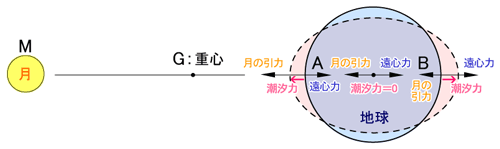
(3)fr=G・M/r2
となる。
rは、月の重心から質点までの距離である。
地球の重心では、
(4)d=r, fd=fr
となるが、ほかの点では過不足が生じる。
この過不足が潮汐を起こす潮汐力である。(図3)
地球の重力は,いま考えている範囲内では地球表面上でこでも同じなので、潮汐力と直接的な関係はない。
ここでfdとfrを水平成分と鉛直成分に分けて潮汐力の各成分を計算すると、
(5)水平成分:fTh=frh-fdh=G・M(sinθ'/r2-sinθ/d2)
(6)鉛直成分:fTv=frv-fdv=G・M(cosθ'/r2-cosθ/d2)
となる。
ここで、θ'およびθ、rとdは図4のとおりである。
図4
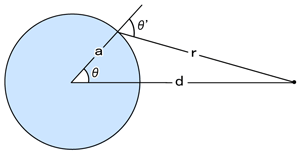
この図から地球の半径をaとすると、
(7)sinθ'=sin(180-θ)=d・sinθ/r
(8)cosθ'=(d・conθ-a)/r
となり、これを(5)、(6)に代入すると、
(9)fTh=G・M/d2・sinθ(d3/r3-1)
(10)fTv=G・M/d2・{(d3/r3-1)cosθ-d3/r3・a/d}
となる。
さらに、図4の三角形の余弦定理から、
r2=d2{1+(a/d)2-2(a/d)cosθ}
となり、a/dは微少量なので、高次の項を省略して、
(11)d3/r3={1+(a/d)2-2(a/d)cosθ}-3/2≒1+3(a/d)cosθ
となるから、(9)、(10)式は、結局、
(12)fTh≒3/2・G・M/d3・a・sin2θ
(13)fTv≒3・G・M/d3・a・(cos2θ-1/3)
となる。
この力は、次のような潮汐ポテンシャル
(14)W=3/2・G・M/d3・a2(cos2θ-1/3)
を水平または鉛直方向に微分することによって導き出される。
海面が潮汐力といつも平衡してバランスを保っているとすると、海面の形は潮汐ポテンシャルと同型になり、(14)式で与えられる。
これを平衡潮汐という。
ところで、地球表面上の単位質量に働く平均的な重力gを考えると、
(15)g=G・E/a2
となる。
これを使って、(14)式を変形すると、
(16)W=3/2・g・(M/E)・(a/d)3・a(cos2θ-1/3)
=2・D・(c/d)3・(cos2θ-1/3)
(17)D=3/4・g・(M/E)・(a/c)3・a
となる。
ここで、cは地球と月の平均よりであり、c/dはその変化率を示す。
すなわち、Dは潮汐力を起こす天体毎に決まる定数であり、(16)式は、潮汐現象を起こすのが、距離の変化c/dと天体の見える角度の変化θであることを示している。
ちなみに、太陽の場合のDを月のものと比較すると、約0.459Dで与えられる。
天体の直下点の経緯度を(α'、δ)、観測点の経緯度を(α、φ)とする。
図5
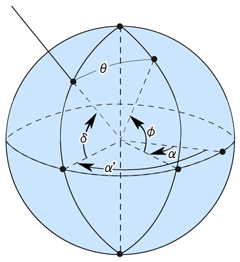
観測点を通る子午線と天体を通る子午線の間の核を時角Tと呼び、T=α'-αとなる。
cosθは、Tとφ、δを使って、
(18)cosθ=cosφcosδcosT+sinφsinδ
と表すことができる。
これを(1)式に代入して、整理すると
(19)W=D・(c/d)3{cos2φ・cos2δ・cos2T+sin2φ・sin2δ・cosT+3(sin2φ-1/3)・(sin2δ-1/3)}
となる。
時角Tは、地球の自転と天体の運行によってほぼ1日で360度変化する。
すなわち、{}の中の各項は、
第1項:半日周期、cos2Tで表される1日2回の周期成分
第2項:1日周期、cosTで表される1日1回の周期成分
第3項:長期周期、Tで関係せず、1日ほとんど一定の成分
に分けられる。
このような潮汐現象を構成する各周期成分のことを分潮という。
しかし、このような分潮に分けたとしても、それぞれの係数は、(c/d)3・cos2δのように時間的に一定でない。
そこで、三角関数の公式を用いて、
(20)cos2δ・cos2T=(1+cos2δ)/2・cos2T
=1/2cos2T+1/2cos2δ・cos2T
=1/2cos2T+1/4cos(2T+2δ)+1/4cos(2T-2δ)
というように、より詳しい分潮に分ける。
このことを潮汐ポテンシャルの展開と呼ぶ。
地球と月または太陽との相互の関係の基本的な変化としては、約1日、1月、1年周期があげられる。
従って、潮汐現象を分潮毎に論ずる時には、半日周期というような言い方が行われるが、当然、この分潮の振幅は月や太陽の位置によって変化するものであることを考慮して置く必要がある。
分潮の展開にはcos関数が使われ、その引数は天文引数(astronomical argment)と呼ばれる。
展開がsin関数となる時は、引数に90度を加減している。
天体の位置は、太陽(地球)の軌道(黄道)面に準拠した黄経・黄緯によって表すが、軌道傾斜や昇交点(各天体の軌道が黄道を南から北に横切る点)、近地点(各天体の軌道の地球と最も近い点)、さらに離心率がわかっていれば、各軌道要素の黄経のみで示すことができる。
従って、地球の自転に関係した時角と各要素の黄経を使って、各分潮の天文引数Vは、
(21)V=V(a1、a2、a3、a4、a5、a6)
=a1T+a2s+a3h+a4p+a5N+a6ps
と表される。
ここで、Tは平均太陽の時角、sは月の平均黄経、hは太陽の平均黄経、pは月の近地点の平均黄経、Nは月の昇交点の平均黄経、psは太陽の近地点の平均黄経である。
a1~a6は、整数のパラメータである。
すなわち、各天文引数Vは、6個の天体の運行に基づく基本的な角度を整数倍した組み合わせによって算出される。
このようにして、6個のパラメータによって展開された数百の分潮が知られているが、海洋潮汐の場合、実用的に大きい振幅を持つのは十数文長に過ぎない。
天体の運行及び時刻系についての詳しい説明は、水路部から毎年発行されている天体位置表(書誌第684号)を参照されたい。
ここでは、潮汐計算に必要な説明にとどめる。
平均太陽は、天の赤道上を一定の速度で動くと仮想された太陽で、その時角は、1日24時間で360度、1時間で15度の割合で変化する。
太陽の平均黄経h及び太陽の近地点の平均黄経psは、
(22)h=280.466449+0.985647360d+0.0003036T2
(23)ps=282.937348+0.0000470783d+0.0004597T2
で概算される。
ここでTは2000年1月1.5日(1月1日12時UT)からの時間経過を36525日単位で測ったもの、dは同じく日単位で測ったものである。
月の平均黄経s、月の近地点の平均黄経p、月の昇交点の平均黄経Nは、
(24)s=218.316656+13.17639647754d-0.001330T2
(25)p=83.353243+0.11140352392d-0.010324T2
(26)N=125.044556-0.05295376276d+0.002076T2
で計算される。
潮汐計算では、天体の位置計算ほどの高い精度は要求されないので、高次の項T2を省略し、さらに、時間の元期を2000年1月1日0時UTに直して、
(27)s=211.728+129.38471(Y-2000)+13.176396(D+L)
(28)h=279.974-0.23871(Y-2000)+0.985647(D+L)
(29)p=83.298+40.66229(Y-2000)+0.111404(D+L)
(30)N=125.071-19.32812(Y-2000)-0.052954(D+L)
(31)ps=282.937+0.01718(Y-2000)+0.000047(D+L)
の略算式を用いる。
ここで、Y=西暦年、D=Y年における1月1日からの経過日数、L=[(Y+3)/4]-500=Y年の年初と2000年年初の間の閏日の数、ただし、[]は中の値の整数部分を表し、2000年以前はマイナスの数として数える。
例えば、1994年はL=[(1994+3)/4]-500=[499.25]-500=499-500=-1となる。
潮汐計算の基礎式は、
(32)W=ΣWi・cos(Vi)
と表される。
ここで、WiとViは天体の理論から導き出される各分潮の振幅と、位相角を表す天文引数である。
添え字iは、分潮の種類を表し、Σは各分潮の和を示す。
海洋潮汐の場合、一年程度の期間の推算やデータ解析をすることが多いので、6個の基礎引数のうち長い周期で変化するNやpsは、分潮の分類には使わず、a1~a4の4個のパラメータで表す。
psは一定の283度(2000年の近似値)、Nは振幅と位相に対する補正fi, uiとして表す。
すなわち、
(33)W=ΣfiWi・cos(Vi+ui)
となる。
psはViの中の定数項に含ませる。
fiとui、すなわちNは、計算期間中は一定と仮定する。
そのため、計算期間は1年以下とし、Nによるfi, Uoの値は、通常、計算期間の中央日としている。
(32)、(33)の式によれば、潮汐現象は各分潮を表す三角関数の和によって表現されているので、この式に基づく会席や推算のやりかたを調和法と呼ぶ。
天体の運行に基づく平衡潮汐に対して、実際の海で起きている潮汐は、海水の運動による慣性や地形の影響を受けて、振幅の増減や位相の遅れ進みが生じる。
そこで、実際の潮汐をηとして、(32), (33)の式を考慮して、
(34)η=ΣHi・cos(Vi-κi)+Zo=ΣfiHi・cos(Vi+ui-κi)+Zo
で表す。
ここで、Hi、κiは、潮汐の観測値から計算された振幅と遅角で、潮汐の調和定数と呼ぶ。
Zoは、平均水面の高さで、本サイトでは海図の水深の基準面からの高さを採用している。
従って、海図の水深値にηを加えることにより、その時の海面から海底までの深さを求めることが出来るようになっている。
また、観測値から各分潮のHi、κiを算出することを調和分解と称する。
本サイトでは、各地のHi、κiを掲げている。
第1表は、海洋潮汐の場合に用いられる各分潮の引数Viのパラメータ(a1、a2、a3、a4)と定数項c、Nの補正、ならびに相対振幅を表している。
ここで、Tは平均太陽の時角から12時間(180°)ずらして、世界時UTに対応する角度になおし、定数項には補正量を含ませてある。
例えば、31番目のM2分潮のT, s, h, p, cに対する係数パラメータは、2、-2、2、0、0だから、
(35)Vi=2T-2s+2h+0p+0(c)
=2T-2s+2h
として計算される。
fi, uiの欄は、第2表によって計算された値を使うことを示している。
相対振幅に*が記されているものは、流体力学的に各分潮が重なり合ってできた複合潮や倍潮を示しており、その振幅は天体の動きに基づく潮汐力からは計算することができない。
備考欄に**とされているものは、気象の影響の大きいものを示している。
ある時刻のfi, uiは、Nの三角関数の級数として表されており、第2表に従って計算する。
L2とM1については、Nとpの組み合わせによる三角関数の和となっている。
例えば、ある時刻のM2のfi, uiを求めるには、最初に(30)式によりNを計算し、さらに第2表の各三角関数の係数を使って、
(36)fM2=1.0004-0.0373cosN+0.0002cos2N+0.0000cos3N
(37)uM2=-2.14sinN+0.00sin2N+0.00sin3N
として計算される。
L2とM1については、fcosuとfsinuをそれぞれ計算してから、
(38)f=square root((fcosu)2+(fsinu)2)
(39)uM2=arctan(fsinu/fcosu)
によって計算する。
ちなみに、Nは1年に19.3度しか変化せず、しかも第2表のように振幅の大きいM2潮などの係数は小さく、係数の大きいOO1潮などは振幅が小さいので、1年以内のfi, uiの変化は、便宜上、無視している。
各分潮の角速度σiは、天体の運行に基づくT, s, h, pの1時間あたりの変化、すなわち、
(40)T/hour=15°/h
(41)s/hour=0.54901652°/h
(42)h/hour=0.04106864°/h
(43)p/hour=0.00464181°/h
を第1表に従って組み合わせて計算される。
例えば、M2潮の角速度は、第1表の各係数が2, -2, 2, 0だから、
(44)σi=2*15-2*0.54901652+2*0.04106864+0*0.00464181
=28.98410424°/h
となる。
各分潮の平衡潮の振幅は、第1表の振幅の係数に、
(45)定数=3/2・M/E・a3/c3・a=0.536m
及び緯度に関する変化係数、
(46)長周期潮=3/4・(1/3-sin2φ)
(47)日周期=1・2・sin2φ
(48)半日周期=1/2・cos2φ
を乗ずることによって得られる。
例えば、30°Nの地点のM2潮の振幅は、第1表の係数が0.908だから
(49)w=0.908*0.536*1/2・cos230=0.18m
となる。
(1)ある日の潮汐を計算するには、まず、0:00UT(世界時)のs, h, p, Nを求め、Vi, uiを計算する。
この時、Tは世界時に対応するようにしているので、T=0°となり、これを添え字0で表すことにして、角分潮の0:00UTの天文引数Vi, uiは、次の式で書ける。
(50)(Voi+Ui)=a2s+a3h+a4p+c+ui
となる。
(2)0:00UTにおける観測点での天文引数Vi, uiは、観測点の経度をL(西経+、東経-)とすると観測点からグリニジ子午線までの角度は-Lとなるので、観測点での天文引数は添え字Lで表して、
(51)(Voi+ui)L=(Voi+ur)-n・L
となる。
ここで、nは、第1表の時角の係数aiであり、各分潮記号の添え字になっているのでサフィックスと呼ばれる。
(3)t:00UTにおける各分潮の位相は、各分潮毎に一定の角速度で進んでゆくので、
(52)(Voi+ui)L+σi・t(UT)=(Voi+ui)-n・L+σi・t(UT)
となる。
(4)各国の標準時をt:00(ST)、時差をSとすると、
(53)t(UT)=t(ST)+S
となり、t:00(ST)における各分潮の天文引数は
(54)[Vi+ui]t:00(ST)=(Voi+ui)-n・L+σi・S+σi・t(ST)
となる。
(5)以上により、経度L(西経+、東経-)、標準時の時差Sの地点のある時刻t(ST)の潮汐は、
(55)η(t)=ΣfiHi・cos([Viui]-κi)
(56)[Vi+ui]={(Voi+ui)-n・L+σi・S}+σi・t(ST)
で計算される。
すなわち、その日の0:00UTにおける。
s, h, p, Nを計算して第1、2表からfi, uiとVoiを算出する。
次に経度と標準時の補正を加えて0:00STにおける天文引数{(Voi+ui)-n・L+σi・S}を計算する。
その地の調和定数Hiとκiは、本表から既知であるから、あとは(55),(56)式に従って各分潮の位相角を進めて、各時刻の潮汐を計算することができる。
(6)長期間の計算を行うときは、fi, uiは計算期間の中央で算出する。
この計算は、fi, uiを期間中一定とした略算なので、1年以上にわたるような長期間の計算では、いくつかの期間に分かれて計算する。
1994年4月1日の名古屋港の潮汐を計算する。
(1)1994年4年1月0:00UTのs, h, p, Nを求め、fi, uiを計算する。
Y=1994, D=31+28+31=90, L=[(1994+3)/4]-500=-1を(27)-(30)式に代入して、
s=211.728+129.38471(Y-2000)+13.176396(D+L)=248.119
h=279.974-0.23871(Y-2000)+0.985647(D+L)=9.129
p=83.298+40.66229(Y-2000)+0.111404(D+L)=209.239
N=125.071-19.32812(Y-2000)-0.052954(D+L)=236.327
これを使って、Voiとfi, uiを計算する。
例えばM2潮のfi, uiは、(36),(37)式から、
fM2=1.0004-0.0373cosN+0.0002cos2N+0.0000cos3N
=1.021
uM2=-2.14sinN-0.00sin2N+0.00sin3N
=1.781
となり、第1表から
Voi=2T-2s+2h=0-2*248.119+2*9.129=242.020
となる。
本サイトに収録した名古屋港の位置や調和定数の値は、
35°05'N, 136°53'E, M2潮、H=65.4cm, κ=179.2°
だから、M2潮の引数は、n=2, s=-9(日本標準時)を使って、
[Vi+ui]=κi=(Voi+ui)-n・L+σi・S+σi・t-κ
=(242.020+1.781)-2*(-136.88)+28.98410424*(-9)+28.98410424・t-179.2
=28.98410424・t+77.5
となる。
従って、この日t時のM2潮は、
η=fiHi・cos([Vi+ui]-κi)
=1.021・65.4cos(σi・t+77.5)
=66.77con(28.9841024・t+77.5)
で計算される。
残りの分潮についてもこの計算式を繰り返し、それを合計することによって、潮汐の推算値が得られる。
13節の(53)式において、経度と標準時は、その場所毎に決まっているので、計算日時には関係しない。
そこで(56)式を変形して、
(57)[Vi+ui]-κi=(Voi+ui)-n・L+σi・S+σi・t-κi
=(Voi+ui)+σi・t-(κi+n・L-σi・S)
=(Voi+ui)+σi・t-gi
(58)gi=κi+n・L-σi・S
とする。
giは、修正遅角と呼ばれる。
giをあらかじめ計算しておけば、fi, ui、とVoiは、場所によらず日時だけによるので、計算がさらに簡略化される。
潮汐に関する本の中には、遅角としてgiをあげているものがあるのでκiと混同しないように注意されたい。
また、(57)式で使っているtは、地方標準時(ST)で、使用する標準時が変わるとgiも変わることに注意されたい。
各地の高潮や低潮の時刻の差を見るには、giが便利である。
比較する地点を添え字i、2で表すと、潮時差Δtは、
σi・Δt=gi1-gi2
=(κi1+n・Li-σi・Si)-(κi2+n・L2-σi・S2)
=κi1-κi2+n・(L1-L2)-σi・(Si-S2)
Δt={κi1-κi2+n・(L1-L2)}/σi-(Si-S2)
となる。
この時間差には、時差もふくまれている事に注意されたい。
一般に使われている潮時差は、卓越する分潮の遅角によって算出される。
日本沿岸では、M2潮によることが多い。
潮汐の進行状況を見るには、統一した自国を用いる必要がある。
世界時UTを使った予報式は、(52)式から
[Vi+ui]-κi=(Voi+ui)-n・L-κi=(Voi+ui)-κo
κo=κi+n・L
となり、κの代わりにκoを用いる。
基準天体がグリニジ子午線上にある時からの遅れ角であることから、κGと表す。
日本では、標準子午線135°Eを基準として、
Δto=κo/σi、κo=κi+n・(L-Lo)、Lo=-135
すなわち、基準天体が標準子午線135°Eの上にきた時からの時間差Δtoによって表すことが多い。
ちなみに、潮汐表第1巻(書誌第781号)の同時潮図は、M2潮のΔtoの分布を描いている。
以上のように、潮汐調和定数の遅角には、いろいろな表現があるのでそれぞれの使い方について注意されたい。
| 記号 | Vi(a1, a2, a3, a4) | Nの補正 | 相対振幅 | 備考 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T | s | h | p | c. | fi | ui | Wi | |||
| 1 | Sa | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0.012 | **太陽年周潮 |
| 2 | Ssa | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 0.073 | **太陽半年周潮 |
| 3 | Mm | 0 | 1 | 0 | -1 | 0 | fMm | uMm | 0.083 | 太陰月周潮 |
| 4 | MSf | 0 | 2 | -2 | 0 | 0 | fM2 | -uM2 | 0.014 | S2-M2 |
| 5 | Mf | 0 | 2 | 0 | 0 | 0 | fMf | uMf | 0.156 | 太陰半月周潮 |
| 6 | 2Q1 | 1 | -4 | 1 | 2 | 270 | fO1 | uO1 | 0.010 | |
| 7 | σ1 | 1 | -4 | 3 | 0 | 270 | fO1 | uO1 | 0.012 | |
| 8 | Q1 | 1 | -3 | 1 | 1 | 270 | fO1 | uO1 | 0.072 | 主太陰楕率潮 |
| 9 | ρ1 | 1 | -3 | 3 | -1 | 270 | fO1 | uO1 | 0.014 | |
| 10 | O1 | 1 | -2 | 1 | 0 | 270 | fO1 | uO1 | 0.377 | 主太陰日周潮 |
| 11 | MP1 | 1 | -2 | 3 | 0 | 90 | fM2 | uM2 | * | M2-P1 |
| 12 | M1 | 1 | -1 | 1 | 0 | 90 | fM1 | uM1 | 0.040 | 副太陰楕率潮 |
| 13 | χ1 | 1 | -1 | 3 | -1 | 90 | fJ1 | uJ1 | 0.006 | |
| 14 | π1 | 1 | 0 | -2 | 0 | 193 | 1 | 0 | 0.010 | 主太陰楕率潮 |
| 15 | P1 | 1 | 0 | -1 | 0 | 270 | 1 | 0 | 0.176 | 主太陰日周潮 |
| 16 | S1 | 1 | 0 | 0 | 0 | 180 | 1 | 0 | 0.004 | ** |
| 17 | K1 | 1 | 0 | 1 | 0 | 90 | fK1 | uK1 | 0.531 | 日月合成日周潮 |
| 18 | ψ1 | 1 | 0 | 2 | 0 | 167 | 1 | 0 | 0.004 | 副太陰楕率潮 |
| 19 | φ1 | 1 | 0 | 3 | 0 | 90 | 1 | 0 | 0.008 | 2次太陰日周潮 |
| 20 | θ1 | 1 | 1 | -1 | 1 | 90 | fJ1 | uJ1 | 0.006 | |
| 21 | J1 | 1 | 1 | 1 | -1 | 90 | fJ1 | uJ1 | 0.030 | 小太陰楕率潮 |
| 22 | SO1 | 1 | 2 | -1 | 0 | 90 | fO1 | -uO1 | 0.005 | |
| 23 | OO1 | 1 | 2 | 1 | 0 | 90 | fOO1 | uOO1 | 0.016 | 2次太陰日周潮 |
| 24 | OQ2 | 2 | -5 | 2 | 1 | 180 | (fO1)2 | uO1*2 | * | |
| 25 | MNS2 | 2 | -5 | 4 | 1 | 0 | (fM2)2 | uM2*2 | * | |
| 26 | 2N2 | 2 | -4 | 2 | 2 | 0 | fM2 | uM2 | 0.023 | 2次太陰楕率潮 |
| 27 | μ2 | 2 | -4 | 4 | 0 | 0 | fM2 | uM2 | 0.028 | 太陽二均差潮 |
| 28 | N2 | 2 | -3 | 2 | 1 | 0 | fM2 | uM2 | 0.174 | 主太陰楕率潮 |
| 29 | ν2 | 2 | -3 | 4 | -1 | 0 | fM2 | uM2 | 0.033 | 主太陰出差潮 |
| 30 | OP2 | 2 | -2 | 0 | 0 | 180 | fO1 | uO1 | * | |
| 31 | M2 | 2 | -2 | 2 | 0 | 0 | fM2 | uM2 | 0.908 | 主太陰半日周潮 |
| 32 | MKS2 | 2 | -2 | 4 | 0 | 0 | fM2*fK2 | uM2+uK2 | * | |
| 33 | λ2 | 2 | -1 | 0 | 1 | 180 | fM2 | uM2 | 0.007 | 副太陰出差潮 |
| 34 | L2 | 2 | -1 | 2 | -1 | 180 | fL1 | uL2 | 0.026 | 副太陰楕率潮 |
| 35 | T2 | 2 | 0 | -1 | 0 | 283 | 1 | 0 | 0.025 | 主太陰楕率潮 |
| 36 | S2 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0.423 | 主太陰半日周潮 |
| 37 | R2 | 2 | 0 | 1 | 0 | 257 | 1 | 0 | 0.004 | 副太陰楕率潮 |
| 38 | K2 | 2 | 0 | 2 | 0 | 0 | fK2 | uK2 | 0.115 | 日月合成半日潮 |
| 39 | MSN2 | 2 | 1 | 0 | -1 | 0 | (fM2)2 | uM2*2 | * | |
| 40 | KJ2 | 2 | 1 | 2 | -1 | 180 | fK1*fJ1 | uK1+uJ1 | * | |
| 41 | 2SM2 | 2 | 2 | -2 | 0 | 0 | fM2 | -uM2 | * | |
| 42 | MO3 | 3 | -4 | 3 | 0 | 270 | fM2*fO1 | uM2+uO1 | * | |
| 43 | M3 | 3 | -3 | 3 | 0 | 180 | (fM2)3/2 | uM2*1.5 | * | |
| 44 | SO3 | 3 | -2 | 1 | 0 | 270 | fO1 | uO1 | * | |
| 45 | MK3 | 3 | -2 | 3 | 0 | 90 | fM2*fK1 | uM2+uK1 | * | |
| 46 | SK3 | 3 | 0 | 1 | 0 | 90 | fK1 | uK1 | * | |
| 47 | MN4 | 4 | -5 | 4 | 1 | 0 | (fM2)2 | uM2*2 | * | |
| 48 | M4 | 4 | -4 | 4 | 0 | 0 | (fM2)2 | uM2*2 | * | |
| 49 | SN4 | 4 | -3 | 2 | 1 | 0 | fM2 | uM2 | * | |
| 50 | MS4 | 4 | -2 | 2 | 0 | 0 | fM2 | uM2 | * | |
| 51 | MK4 | 4 | -2 | 4 | 0 | 0 | fM2*fK2 | uM2+uK2 | * | |
| 52 | S4 | 4 | 0 | 0 | 0 | 0 | 1 | 0 | * | |
| 53 | SK4 | 4 | 0 | 2 | 0 | 0 | fK2 | uK2 | * | |
| 54 | 2MN6 | 6 | -7 | 6 | 1 | 0 | (fM2)3 | uM2*3 | * | |
| 55 | M6 | 6 | -6 | 6 | 0 | 0 | (fM2)3 | uM2*3 | * | |
| 56 | MSN6 | 6 | -5 | 4 | 1 | 0 | (fM2)2 | uM2*2 | * | |
| 57 | 2MS6 | 6 | -4 | 4 | 0 | 0 | (fM2)2 | uM2*2 | * | |
| 58 | 2MK6 | 6 | -4 | 6 | 0 | 0 | (fM2)2*fK2 | uM2*2+uK2 | * | |
| 59 | 2SM6 | 6 | -2 | 2 | 0 | 0 | fM2 | uM2 | * | |
| 60 | MSK6 | 6 | -2 | 4 | 0 | 0 | fM2*fK2 | uM2+uK2 | * | |
| fiの係数 | uiの係数 | ||||||
|---|---|---|---|---|---|---|---|
| 1. | cosN | cos2N | cos3N | sinN | sin2N | sin3N | |
| Mm | 1.0000 | -0.1300 | 0.0013 | 0.0000 | 0.00 | 0.00 | 0.00 |
| Mf | 1.0429 | 0.4135 | -0.0040 | 0.0000 | -23.74 | 2.68 | -0.38 |
| O1 | 1.0089 | 0.1871 | -0.0147 | 0.0014 | 10.8 | -1.34 | 0.19 |
| K1 | 1.0060 | 0.1150 | -0.0088 | 0.0006 | -8.86 | 0.68 | -0.07 |
| J1 | 1.0129 | 0.1676 | -0.0170 | 0.0016 | -12.94 | 1.34 | -0.19 |
| OO1 | 1.1027 | 0.6504 | 0.0317 | -0.0014 | -36.68 | 4.02 | -0.57 |
| M2 | 1.0004 | -0.0373 | 0.0002 | 0.0000 | -2.14 | 0.00 | 0.00 |
| K2 | 1.0241 | 0.2863 | 0.0083 | -0.0015 | -17.74 | 0.68 | -0.04 |
| L2 | f cos u=1-0.2505cos2p-0.1102cos(2p-N) | -0.0156cos(2p-2N)-0.0370cosN | |||||
| f sin u=-0.2505sin2p-0.1102sin(2p-N) | -0.0156sin(2p-2N)-0.0370sinN | ||||||
| Mi | f cos u=2cosp+0.4cos(p-N) | ||||||
| f sin u=sinp+0.2sin(p-N) | |||||||

| 2019/07 | WAF設定 |
|---|---|
| 〃 | キャッシュ設定 |
| 2019/07 | 潮汐画像API |
| 2019/06 | 潮汐カレンダー |
| 2019/05 | リニューアル |
| 〃 | スマフォ対応 |
| 2019/05 | XSERVERへお引越し |
対応済潮汐表
通年日算出に不具合がありました。既に改修完了し本番適用いたしております。
ご迷惑をおかけしまして申し訳ありませんでした。
対応済スマフォ不具合
リストボックスにて選択したものと違うのが選択される。
原因は、Materialize CSS + iOS13による不具合と判明。既に改修完了し本番適用いたしております。
ご迷惑をおかけしまして申し訳ありませんでした。
お気軽にお問い合わせください。
※ユーザーの皆様からお寄せいただくご意見・ご要望を参考に、より良いサービス・機能を提供できるよう努めております。
ご自由にご利用ください。
(グラフやリンクもご自由に)
※免責事項
本データによって生じるいかなる不具合、トラブルや損害の責任を負いかねますので、自己責任でのご利用をお願いします。
当サイトでは、クッキー(Cookie)を使用しています。
※より使いやすいウェブサイトの実現を目的とするものであり、お客様のプライバシーを侵害するものではなく、またお客様のコンピューターへ悪影響を及ぼすことはありません。
当サイトでは、Google AdSenseを利用しています。
※サイト運営(ドメインやレンタルサーバー費用等の捻出)のため、何卒ご理解いただきますようお願いいたします。
S44年生まれ。滋賀県大津市在住。N88にはじまり各種C言語を経て、近年はPHP、jQuery。WEB案件のご依頼などはお気軽にご相談ください。